I have often been forwarded articles like this one
here which is stating the large probability of receiving a false negative on a COVID-19 test.
This, at first light, appears to be a huge problem.
From the article, we have the reported probability of receiving a false positive based on how many days you have had this disease for:
Day 1 of disease: 100% chance of false positive.
Day 4 of disease: 67% chance
After symptoms begin to show (When you would likely then go to get a test)
Day 5 of disease 38%
Day 8 of disease 20%
As I said, this appears to be frightening. Of those getting the test (who have symptoms) something close to 2 out of 5 tests will say that the person is COVID negative when in fact they have the disease.
So let's work through this. Let's say that you are sick (or someone in your family is sick) and you decide to get a COVID test. You go through the process, get your brain tickled, then get the phone call later that evening. Good News. The result is negative.
But then you read this article. Are you actually COVID free? or did you just receive a false negative? What is the likelihood that you actually have COVID given that you received a negative test result?
Well, we can actually work this out quite easily.
Let's first utilize our general multiplication rule for events that are not mutually exclusive:
This says that the probability that both events A and B occur is the probability of A occurring multiplied by the probability of event B occurring, given that, A has already occured. To put this into a more straight forward sense:
Let suppose you have a cooler of beverages. 3 colas and 4 rootbeers. The probability you reach in (without looking) and pull out a cola and a rootbeer is a probability you pull out a cola and then the probability you pull out a rootbeer, given that, you have already pulled out a cola.
Now the important piece to remember is that this goes both ways.
The probability, P(Cola and Rootbeer) is identical to the opposite P(Rootbeer and Cola). that is, the order is not necessarily important, as long as we finish with one of each.
Thus we have that:
Why is this helpful to us?
Almost there - let's open this up, define (A) and (B), and then things should start to become clear.
Where if we set: (A) = "Covid" or (C) and (B) = "Negative test" or (N) we obtain:
From here we can work through what we know (or can find out) in order to answer our question.
What was our question again?
What is the likelihood that you actually have COVID given that you received a negative test result?
Right, that is, we are looking for P(C|N) so we need to determine values for all the other variables:
So how do we go about solving all this?
Well, let's start out with P(C). Currently, there are just over 100k active cases in BC. Given a population of just over 5 million that puts you at about a 2.5% chance of having COVID. Yes, exposures, or area in which you live/work/play is going to impact this, but we don't have that, so let's keep it simple.
Let's then take a look at P(N). in total, just over 2 million tests have been done in BC (2 336 090), with just over 200K of those being a positive result (217 485) that is we can work out the P(+) to be 9.3%. Using our compliment rule, we can then obtain the P(N) to be 1-P(+) or 90.7%.
Finally, we need to determine the P(N|C) That is, what is the probability you get a negative test result given that you have COVID.
Hey, that is our false-negative rate as reported above. Let's start by using the 38% false negative. so summarizing all this we have:
- P(C) = 0.025
- P(N) = 0.907
- P(N|C) = 0.38
We can then re-arrange our above formula to solve for P(C|N) and then make the appropriate substitutions.
Making our substitutions:
What does this mean? it means that given the low rates of actual COVID occurrence in the province and despite the relatively high rates of false negatives. the probability that you actually have COVID given that you received a False-negative is only 1%. That is reasonably low.
What about if you had a test on day 4 (Pre-symptoms) which when you think about it, is extremely quick for you to realize - notified of an exposure (X) days ago, feeling fine, but will book a test just the same:
Again, despite the alarmingly high false-negative rate. the probability that you actually have COVID given that you received the negative test result is exceptionally low (less than 2%)
Okay; so what is the moral of the story.
Articles like this come out - and they end up breeding fear and distrust of the tests - potentially leading to people not taking the tests at all. They may think the test is not worth it, the results are meaningless. This of course is problematic in determining caseloads, tracking spread, and combating and turning the tides for this disease.
Despite these high rates of false negatives. This is still an extremely useful tool and an extremely valuable resource to utilize in our fight against COVID.
Now - if infection rates were to skyrocket. suppose that instead there was an 80% chance that you had COVID. At that time we would have to question whether or not this test was effective, as the false-negative rate would be extremely problematic. But with our current "low" relative caseloads and infection rates, this large of a false-negative is not a huge concern.



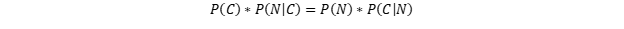




No comments:
Post a Comment